数据结构与算法

算法与数据结构

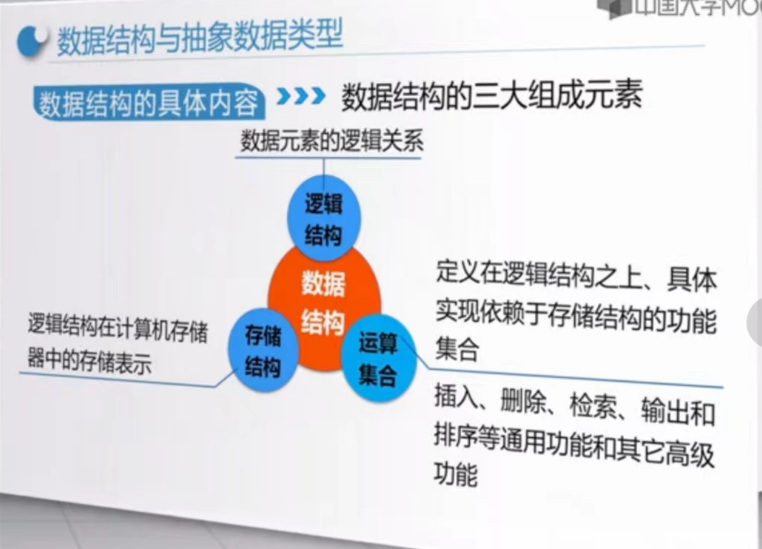
数据结构与抽象数据类型

逻辑结构

可以二元组B=(D,R)表示，其中D是数据元素集合，R是D中数据元素间关系集合

问题决定逻辑结构

线性结构：

图状结构：

树形结构：

存储结构

数据的逻辑结构是独立于计算机的，它与数据在计算机中的存储无关，如果将数据在计算机中无规律地存储，是没有用的。

对于一个数据结构B=(K,R),必须建立从结点集合到计算机某个存储区域M的一个映象，这个映象要直接或间接地表达结点之间的关系R

顺序存储

• 将逻辑上相邻的结点存储在连续存储区域M的相邻的存储单元中，使逻辑相邻的节点一定是物理位置相邻
• 数组就是顺序储存的一个典型

链式存储

• 链式存储方式是给每一个结点附加一个指针段，一个结点的指针所指的是该结点的后继的存储地址；
• 一个结点可能有多个后继，所以指针段可以是一个指针，也可以是多个指针。

索引存储

• 元素的地址集中储存在索引区域中，搜索索引区域可以快速获取数据地址。
• 以线性结构为例，设开始结点的索引号为1，其他结点的索引号等于其驱结点的索引号加1，则每一个结点都有唯一的索引号，根据结点的索引号确定该结点的储存地址，进而访问结点数据。
• 字典的索引目录就是索引存储的实例，通过索引可以快速查到所在页码。

散列存储

• 构造一个函数h，实现从集合K到存储区域M的映射；
• 函数的定义域为K，值域为M，K中的每一个结点ki在计算机中的存储地址由h(ki)确定；
• 仅需要计算即可获得数据的存储地址。

运算集合

对于一批数据，数据的运算是定义在数据的逻辑结构上的，而运算的具体实现依赖于数据的存储结构。

• 插入

在一个结构中添加一个新结点。

• 删除

在一个结构中删除一个结点。

• 检索

在一个结构中查找满足条件。

• 输出

将一个结构所有结点的值打印、输出。

• 排序

将一个结构中所有结点按某种顺序重新排列。

抽象数据结构

概念

从机器指令、汇编语言中没有类型的概念，到现在的面向对象程序设计语言中抽象数据类型概念的出现，程序设计经历了一次次抽象，数据的抽象经历了三个发展阶段。

描述

• 是与实现无关的数据类型，是一种数据模型及定于在该模型上的一组运算
• 抽象数据的描述包括给出抽象数据的名称、数据的集合、数据之间的关系和操作的集合等方面的描述