概念

分组密码是一种对称密钥加密算法，它将明文分成固定大小的块（block），然后使用相同的密钥对每个块进行加密。与流密码逐位或逐字节加密不同，分组密码处理的是数据块。

分组密码属于对称密码体制，所以加密开药空间与解密密钥空间相同。在加解密是需要满足一下要求：

分组足够长，假设n为发分组长度，则分组代换表中的字母个数2n足够大才能避免穷举攻击。

秘钥长度足够长，以防止秘钥穷举攻击。

由秘钥确定的置换算法要足够复杂，足以抵抗各种已知攻击。

加解密运算简单，易于软硬件实施快速计算。

一般无数据扩展，即明文与密文长度相同。

雪崩效应

雪崩效应是密码学中的一个重要概念，指的是输入的微小变化会引起输出的巨大变化。在理想情况下，明文或密钥的单个比特的变化应该会影响密文的大约一半的比特。这对于密码算法的安全性至关重要，因为它可以有效地掩盖明文和密钥之间的统计关系，使攻击者难以通过分析密文来推断明文或密钥。

分组加密法的模式

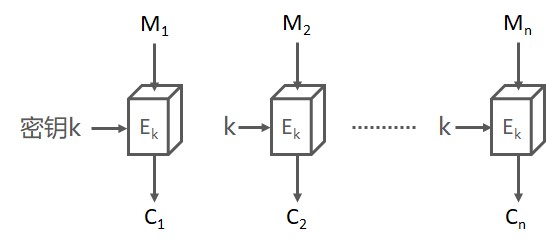
什么是模式分组密码只能加密固定长度的分组，但是我们需要加密的明文长度可能会超过分组密码的分组长度，这时就需要对分组密码算法进行迭代，以便将一段很长的明文全部加密。这个迭代的方法就称为分组密码的模式（mode）。在介绍模式前我们引入两个术语：明文分组（$M_n$）：指分组密码算法中作为加密对象的明文，明文分组的长度与分组密码算法的分组长度是等长的。密文分组（$C_n$）：指使用分组密码算法将明文分组加密之后所生成的密文。

3.2.1 电子编码薄模式（ECB）

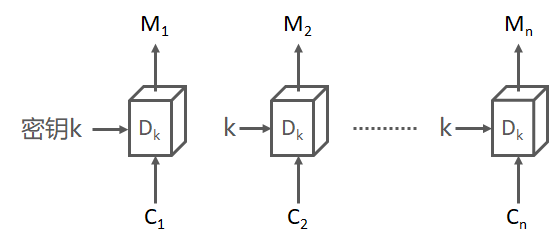
这是分组加密最简单的一种模式，即明文的每一个块加密成密文的每一个块。明文被分为若干块$(M_1,M_2,M_3,M_4, … ,M_n)$，通过加密方法$E_k$，得到密文$(C_1,C_2,C_3,C_4,…,C_n)$，当最后一个明文分组小于分组长度时，需要用一些特定的数据进行填充。

1.6.3 分组密码 - 图2

解密过程也是一次对一个分组解密，而且每次解密都使用同一密钥。 1.6.3 分组密码 - 图3

ECB模式的特点ECB模式是所有模式中最简单的一种。ECB模式中，明文分组与密文分组是一一对应关系，因此，如果明文中存在多个相同的明文分组，则这些明文分组最终都将被转换为相同的密文分组。这样一来，只要观察一下密文，就可以知道明文中存在怎么样的重复组合，并可以以此为线索来破译密码，因此ECB模式是存在一定风险的。
对ECB模式的攻击ECB模式中，每个明文分组都是各自独立地进行加密和解密，但这其实是一个很大的弱点。假如存在一个攻击者，当他作为中间人截获两方的通信时，他能够改变密文的分组顺序，当接收者对密文进行解密时，由于密文分组的顺序被改变了，因此相应的明文分组的顺序也被改变了，那么接收者实际上是解密出了一段被篡改后的密文。在这种场景中，攻击者不需要破译密码，也不需要知道分组密码的算法，他只需要知道哪个分组记录了什么样的数据。思考一个模拟的场景：

假设分组的长度为128比特（16字节），某银行的转账请求数据由以下三个分组构成。分组1：付款人的银行账号分组2：收款人的银行账号分组3：转账金额此时我们模拟一个转账请求数据：从A-5374帐号向B-6671帐号转账1亿元，用16进制数据表示：明文分组1=41 2D 35 33 37 34 20 20 20 20 20 20 20 20 20 20 （付款人：A-5374）明文分组2=42 2D 36 36 37 31 20 20 20 20 20 20 20 20 20 20 （收款人：B-6671）明文分组3=31 30 30 30 30 30 30 30 30 20 20 20 20 20 20 20 （转账金额：100000000）

接下来，攻击者将密文分组1和2的内容进行对调。（此时攻击者并不知道分组的具体内容，但知道这是付款人信息）明文分组2=42 2D 36 36 37 31 20 20 20 20 20 20 20 20 20 20 （收款人：B-6671）明文分组1=41 2D 35 33 37 34 20 20 20 20 20 20 20 20 20 20 （付款人：A-5374）明文分组3=31 30 30 30 30 30 30 30 30 20 20 20 20 20 20 20 （转账金额：100000000）当银行对信息进行解密时，信息的内容实际上已经发生了改变，付款人的身份和收款人的身份已经被调换了。这就是ECB模式的最大弱点，可以在不破译密文的情况下操纵密文。

3.2.2 密码分组链接模式（CBC）

这个模式的实现更复杂、更安全，因此它是使用最普遍的块加密模式。在这种模式下，来自上一块的密文与当前明文块做XOR逻辑运算，得到的结果才是加密的位块。

1.6.3 分组密码 - 图4

如果为每个消息传输选取不同的IV，那么两个相同的消息即使使用相同的密钥，也将有不同的密文。这大大提高了安全性。问题在于：接收端如何知道所使用的IV呢？一种方法是在不安全的通道上发送该IV，并且该IV只使用一次，永不重复。另外一种方法就是基于唯一数的概念。唯一数是一个唯一的数字，永远不重复使用的密钥，它不一定非得保密，它可以是消息的数目等。用块加密法将唯一数加密后生成IV。如果唯一数附加到密文前面，接收端就可以还原IV。

CBC模式的特点在CBC模式中，我们无法单独对一个中间的明文分组进行加密，加入要生成第三组密文，那么至少需要凑齐分组1,2,3才行。观察CBC模式的解密过程，我们发现：如果加密后的分组C2出现内容错误（存储介质故障或者网络传输中的误码等）使得一个分组中的0变成了1。那么解密的时候最多只会让2个分组内容受到数据损坏的影响。

但是，如果不是数据出错，而是密文分组中有比特缺失，那么即使丢失一个比特，也会导致密文分组的长度发生变化，后续的分组发生错位，最终导致后面的所有密文分组都会解密出无效的数据。 1.6.3 分组密码 - 图6

对CBC模式的攻击

比特反转如果攻击者截获了传递信息，在这段信息中包含了初始向量IV，根据CBC模式的解密方式我们可以看出，如果攻击者对IV中的任意比特进行反转（1变为0，0变为1），那么明文中相应的比特位就会发生反转。

对CBC模式的攻击

填充提示攻击填充提示是一种利用分组密码中太难冲部分来进行攻击的方法。在分组密码中，当明文长度不为分组长度的整数倍时，需要在最后一个分组中填充一些数据使其凑满一个分组长度。在填充提示攻击中，攻击者会反复发送一段密文，每次发送时都对填充内容进行少许修改。由于接收者（服务器）在无法正确解密时会返回一个错误消息，攻击者通过这个错误消息就可以获取一部分与明文相关的信息，当然这个方法不仅仅适用于CBC模式，而是适用于所有需要进行分组填充的模式。要防御这种攻击，就必须验证密文是否是由合法的发送者在知道明文内容的前提下生成的。

3.2.3 密文反馈模式（CFB）

在CFB模式中，前一个密文分组会被送回到密码算法的输入端，这里的反馈指的是返回输入端的意思。在ECB模式和CBC模式中，明文分组都是通过密码算法进行加密的，然而，在CFB模式中，明文分组并没有通过密码算法来直接进行加密。 1.6.3 分组密码 - 图8

CFB模式的解密过程如图所示，解密算法和加密的算法是相同的，因为我们可以将CFB模式看作是一种通过分组密码来实现流加密的方式，CFB模式中的密码算法相当于用来生成伪随机数和密文进行XOR运算。通过之前对流密码的学习，我们知道流密码的加密解密的算法是相同。 1.6.3 分组密码 - 图9

对CFB模式的攻击

重放攻击举一个例子：Alice向Bob发送了一条消息，这条消息由4个密文分别组成。攻击者将消息的后3个密文分组保存下来，第二天，Alice又向Bob发送了内容不同的4个密文分组（这里我们假设Alice使用的密钥是没有变的）。攻击者将昨天保存下来的3个分组分别替换了这段密文的后3个分组。当Bob解密的时候，4个分组中只有第一个可以解密成功，而第2组就会产生错误，然而第3和第4则被替换成了攻击者保存下来的之前使用过的分组，Bob仍然可以正常解密。此时第2个分组成为了一个错误的分组，但Bob无法确认是网络传输过程中的通信错误，还是被人篡改的。

3.2.3 密文反馈模式（CFB）

1.6.3 分组密码 - 图10

3.2.4 输出反馈模式（OFB）

这个模式使用分组加密法来生成一个密钥流。密钥和块加密法的初始输入启动这个加密过程，通过将块加密法的输出加密。解密的过程同样是对初始向量做加密运算，将得到的密钥流与密文做XOR运算。 1.6.3 分组密码 - 图11

CFB模式与OFB模式的对比OFB模式和CFB模式的区别仅仅在于密码算法的输入。CFB模式中，密码算法的输入是前一个密文分组，也就是将密文分组反馈到密码算法中，因此就有了“密文反馈模式”这个名字。OFB模式中，密码算法的输入则是密码算法的前一个输出，也就是将输出反馈给密码算法，因此就有了“输出反馈模式”这个名字。

3.2.5 计数器模式（CTR）

CTR模式中，每个分组对应一个逐次累加的计数器，并通过对计数器进行加密来生成密钥流。也就是说，最终的密文分组是通过将计数器加密得到的比特流，与明文分组进行XOR运算得到的。 1.6.3 分组密码 - 图12

计数器的生成方法每次加密是都会生成一个不同的值（nonce）来作为计数器的初始值。例如：当分组长度为128比特（16字节）时，计数器的初始值可能是像这样的形式。

其中，前8个字节为nonce，这个值在每次加密时必须都是不同的。后8个字节为分组序号，这个部分是会在加密的过程中逐次累加的。

66 1F 98 CD 37 A3 8B 4B 00 00 00 00 00 00 00 01 明文分组1的计数器66 1F 98 CD 37 A3 8B 4B 00 00 00 00 00 00 00 02 明文分组2的计数器66 1F 98 CD 37 A3 8B 4B 00 00 00 00 00 00 00 03 明文分组3的计数器66 1F 98 CD 37 A3 8B 4B 00 00 00 00 00 00 00 04 明文分组4的计数器

意义：

扩散性： 雪崩效应体现了密码算法的扩散性，即将明文和密钥的信息扩散到整个密文中。这意味着即使攻击者只知道密文的一部分，也很难推断出明文或密钥的任何信息。
混淆性： 雪崩效应也体现了密码算法的混淆性，即将明文和密钥之间的关系变得复杂和难以理解。这使得攻击者难以通过分析密文来找到明文和密钥之间的统计规律。
抵抗差分密码分析： 雪崩效应使得差分密码分析更加困难。差分密码分析是一种攻击方法，它通过分析明文和密文的微小差异来推断密钥。如果密码算法具有良好的雪崩效应，那么明文的微小差异会导致密文的巨大差异，从而使差分密码分析难以进行。
抵抗线性密码分析： 类似地，雪崩效应也增加了线性密码分析的难度。线性密码分析试图找到明文、密文和密钥之间的线性关系。强大的雪崩效应使得建立这样的线性关系变得更加困难。

实现：

密码算法通常使用多种技术来实现雪崩效应，例如：

S盒（Substitution boxes）： S盒是非线性查找表，可以将输入的比特位映射到输出的比特位。精心设计的 S 盒可以有效地实现雪崩效应。
P盒（Permutation boxes）： P盒用于置换比特位的顺序，可以进一步增强扩散性。
迭代结构： 许多密码算法采用迭代结构，例如 Feistel 网络或 SPN 结构，通过多轮迭代来增强雪崩效应。每一轮迭代都应用 S 盒、P 盒和其他操作，逐步扩散和混淆明文和密钥的信息。